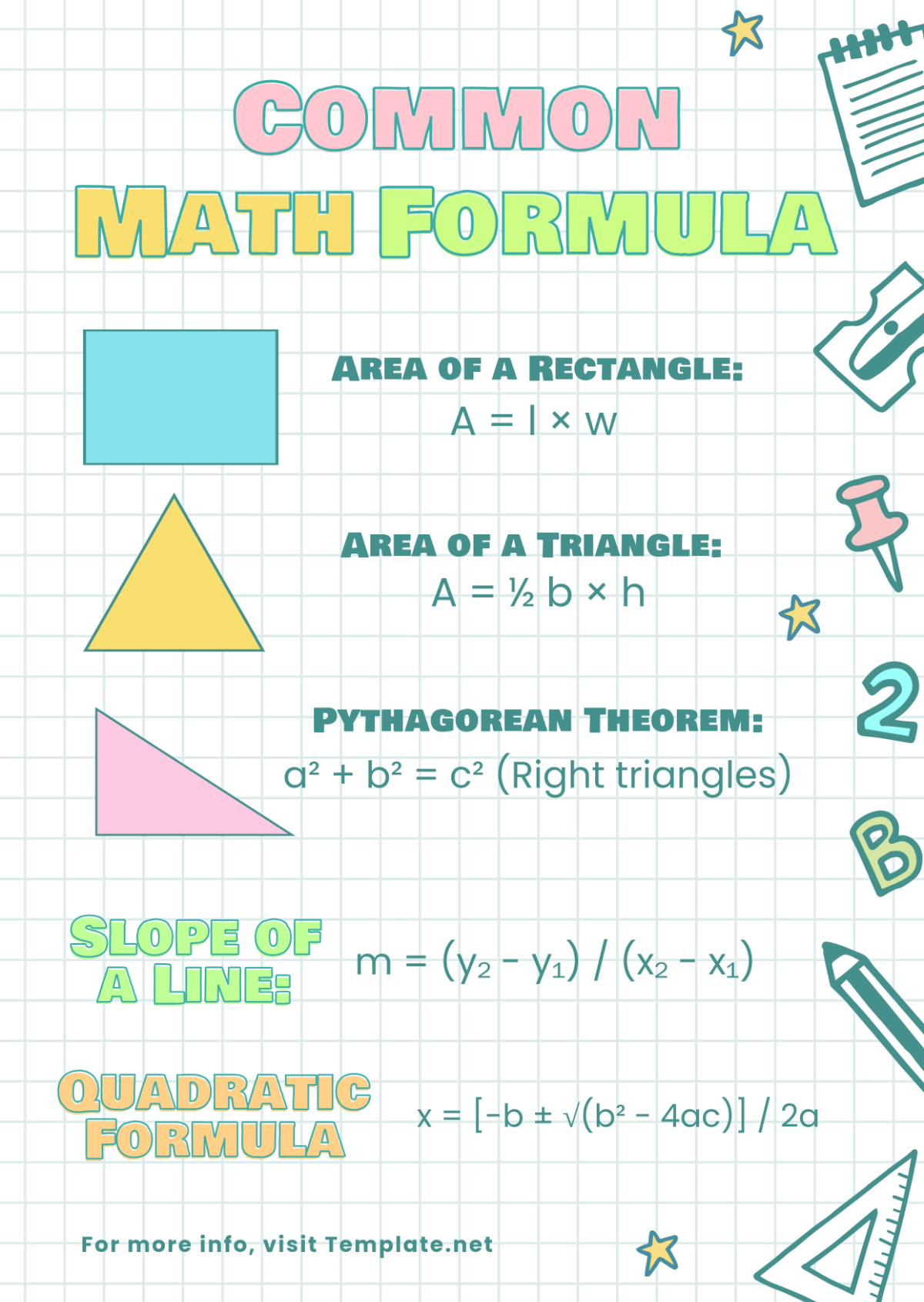Math Study Guide

I. Introduction

Welcome to the comprehensive Math Study Guide. This guide is designed to assist you in mastering the key concepts and principles necessary for success in mathematics. Whether you are a student, educator, or enthusiast, this guide provides a structured approach to learning.

A. Purpose of the Guide

The purpose of this guide is to:

Summarize core mathematical concepts
Provide step-by-step solutions to common problems
Offer practice exercises with solutions
Share tips and strategies for effective learning

B. How to Use This Guide

This guide is structured in a logical flow. Each section builds on the previous one. It's recommended to follow the guide sequentially for the best learning experience.

II. Core Concepts

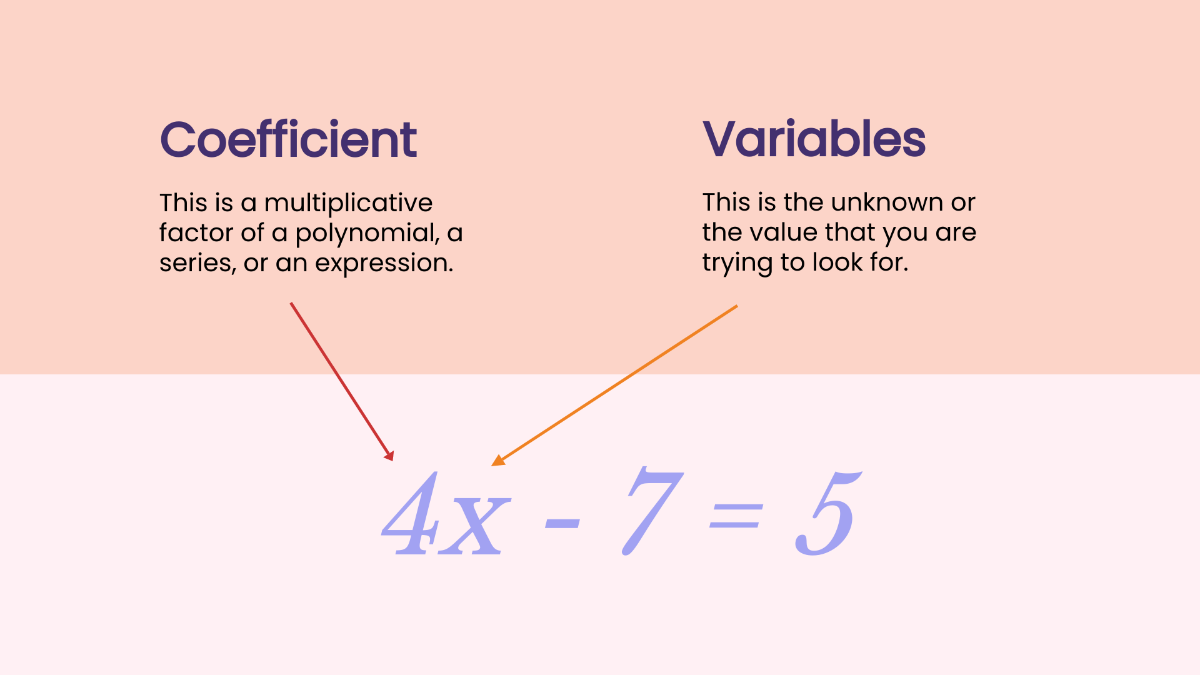
Expressions, Equations, and Inequalities

Basic operations on algebraic expressions: [EXPRESSION OPERATIONS]
Solving linear and quadratic equations: [EQUATION SOLVING]
Inequality notation and solving inequalities: [INEQUALITY TOPICS]

Functions and Graphs

Understanding function notation: [FUNCTION NOTATION]
Graphing linear, quadratic, and exponential functions: [GRAPHING FUNCTIONS]
Analyzing domain, range, and behavior of functions: [FUNCTION ANALYSIS]

Polynomials and Factoring

Operations with polynomials: addition, subtraction, multiplication: [POLYNOMIAL OPERATIONS]
Factoring techniques: common factors, difference of squares, grouping: [FACTORING METHODS]

Angles and Lines

Types of angles: acute, obtuse, right: [ANGLE TYPES]
Properties of parallel and perpendicular lines: [PARALLEL & PERPENDICULAR]
Angle relationships within geometric figures: [ANGLE RELATIONSHIPS]

Triangles and Quadrilaterals

Classifying triangles by sides and angles: [TRIANGLE CLASSIFICATION]
Properties of special triangles: equilateral, isosceles, scalene: [SPECIAL TRIANGLES]
Types of quadrilaterals: parallelograms, rectangles, squares, rhombuses: [QUADRILATERAL TYPES]

Circles and Polygons

Definitions of circle elements: radius, diameter, circumference: [CIRCLE ELEMENTS]
Properties of inscribed and circumscribed angles: [INSCRIBED & CIRCUMSCRIBED ANGLES]
Characteristics of polygons: regular, irregular, convex, concave: [POLYGON PROPERTIES]

Limits and Continuity

Understanding the concept of limits: [LIMITS]
Evaluating limits algebraically and graphically: [EVALUATING LIMITS]
Continuity of functions and the intermediate value theorem: [CONTINUITY & THEOREMS]

Derivatives and Integrals

Calculating derivatives using the limit definition and differentiation rules: [DERIVATIVE CALCULATIONS]
Interpreting the derivative as a rate of change: [DERIVATIVE INTERPRETATION]
Finding antiderivatives and definite integrals: [INTEGRATION]

Applications of Differentiation and Integration

Optimization problems using derivatives: [OPTIMIZATION]
Related rates problems: [RELATED RATES]
Area under curves and applications of integration: [AREA & INTEGRATION APPLICATIONS]

III. Practice Exercises

Practice is essential to mastering mathematical concepts. Try solving the following exercises to test your understanding:

A. Algebra Exercises

Problem

Solution

Find the value of x: [ALGEBRA EXPRESSION 1]

[YOUR SOLUTION FOR ALGEBRA EXERCISE 1]

Simplify: [ALGEBRA EXPRESSION 2]

[YOUR SOLUTION FOR ALGEBRA EXERCISE 2]

B. Geometry Exercises

Problem

Solution

Calculate the area of a triangle with base [TRIANGLE BASE] and height [TRIANGLE HEIGHT].

[YOUR SOLUTION FOR GEOMETRY EXERCISE 1]

Find the perimeter of a rectangle with length [RECTANGLE LENGTH] and width [RECTANGLE WIDTH].

[YOUR SOLUTION FOR GEOMETRY EXERCISE 2]

C. Calculus Exercises

Problem

Solution

Find the derivative of f(x) = [DERIVATIVE EXPRESSION].

[YOUR SOLUTION FOR CALCULUS EXERCISE 1]

Evaluate the integral ∫ [INTEGRAL EXPRESSION] dx.

[YOUR SOLUTION FOR CALCULUS EXERCISE 2]

IV. Tips and Strategies

To enhance your learning experience, consider the following tips. Firstly, [PRACTICE REGULARLY] to reinforce concepts and solidify your understanding of mathematical principles. Consistent practice not only helps in mastering skills but also builds confidence in tackling more complex problems.

Secondly, don't hesitate to [SEEK HELP] from teachers, tutors, or online resources whenever you encounter challenges or need clarification on certain topics. Utilizing additional support can provide valuable insights and explanations to aid in your comprehension.

Thirdly, [FORM STUDY GROUPS] with peers who share similar learning objectives. Collaborating with others allows for the exchange of ideas, discussion of concepts, and mutual support in problem-solving.

Lastly, make use of [EDUCATIONAL TOOLS AND APPS] designed to complement your learning journey. Whether it's interactive tutorials, practice quizzes, or educational games, leveraging technology can make learning more engaging and effective. By incorporating these strategies into your study routine, you can maximize your potential and achieve success in mathematics.

V. Conclusion

We hope this Math Study Guide is beneficial in your learning journey. Remember, consistency and practice are key to mastering mathematics. For any further assistance, feel free to reach out to [YOUR NAME] at [YOUR COMPANY EMAIL].